How To Find Increasing Decreasing Intervals: The Ultimate Guide For Math Enthusiasts

Ms. Kenya Ullrich 13 May 2025

Alright, listen up, folks. If you're here because you're scratching your head over how to find increasing decreasing intervals, you're in the right place. This isn't just another boring math tutorial. No way, no sir. This is the ultimate guide packed with tips, tricks, and all the knowledge you need to ace this concept. Whether you're a student prepping for finals or someone brushing up on calculus, we’ve got your back. Let’s dive in and make sense of those intervals once and for all.

Now, before we get into the nitty-gritty, let's talk about why this matters. Understanding how to find increasing decreasing intervals isn’t just about passing a test—it’s about mastering a fundamental concept in calculus. Think about it. These intervals help us understand how functions behave, which is super important in fields like engineering, economics, and even physics. So yeah, it’s kinda a big deal.

But don’t worry. We won’t overwhelm you with complicated jargon or confusing formulas right off the bat. Instead, we’re going to break it down step by step, make it super easy to digest, and even throw in some fun examples to keep things interesting. Let’s do this!

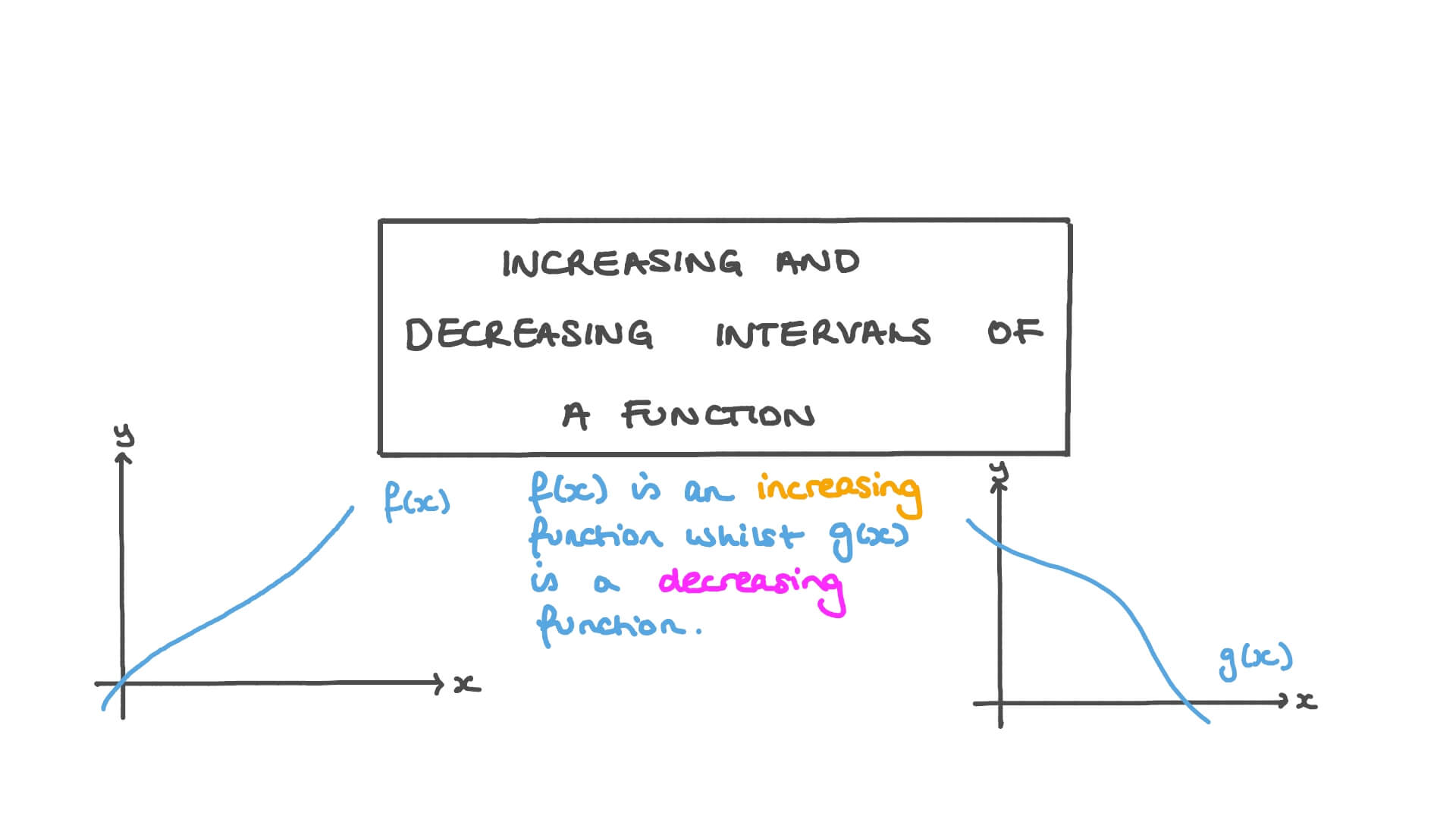
What Are Increasing and Decreasing Intervals Anyway?

Let’s start with the basics, shall we? When we talk about increasing and decreasing intervals, we're referring to how a function behaves over certain ranges of input values. Simply put, if the graph of a function goes up as you move from left to right, it’s increasing. If it goes down, it’s decreasing. Sounds simple enough, right? But there’s more to it than meets the eye.

Key Takeaways:

Increasing intervals mean the function values are getting bigger.
Decreasing intervals mean the function values are getting smaller.
These intervals help us analyze the behavior of functions.

Why Should You Care About Increasing Decreasing Intervals?

Here’s the thing. Learning how to find increasing decreasing intervals isn’t just about acing a math test. It’s about understanding the world around you. Think about it. In real life, functions are everywhere. From predicting stock prices to analyzing population growth, understanding how values change over time is crucial. And that’s where increasing and decreasing intervals come in handy.

Applications in Real Life

Let’s look at a few examples:

In economics, these intervals help predict trends in supply and demand.
In physics, they assist in analyzing motion and velocity.
In business, they’re used to forecast revenue and costs.

So yeah, mastering this concept can open doors to a lot of exciting opportunities. Cool, right?

Step-by-Step Guide: How to Find Increasing Decreasing Intervals

Alright, now that we’ve covered the basics, let’s get into the meat of the matter. Here’s a step-by-step guide to help you find increasing decreasing intervals like a pro:

Step 1: Understand the Derivative

The first step is to calculate the derivative of the function. Why? Because the derivative tells us the rate of change of the function. If the derivative is positive, the function is increasing. If it’s negative, the function is decreasing. Easy peasy, right?

Step 2: Solve for Critical Points

Critical points are where the derivative equals zero or is undefined. These points help us identify where the function might change from increasing to decreasing or vice versa. To find them, set the derivative equal to zero and solve for x.

Step 3: Test the Intervals

Once you’ve identified the critical points, divide the number line into intervals. Then, pick a test point from each interval and plug it into the derivative. If the result is positive, the function is increasing in that interval. If it’s negative, it’s decreasing.

Pro Tip: Always double-check your work. Math can be tricky, but a little extra effort goes a long way.

Common Mistakes to Avoid

Now, let’s talk about some common mistakes people make when finding increasing decreasing intervals:

Forgetting to check for critical points.
Not testing enough intervals.
Misinterpreting the sign of the derivative.

Trust me, these mistakes can trip you up. But with a little practice, you’ll get the hang of it in no time.

Advanced Techniques: Beyond the Basics

Ready to take it to the next level? Here are a few advanced techniques to help you master increasing decreasing intervals:

Using the Second Derivative Test

The second derivative test can help you confirm whether a function is increasing or decreasing. If the second derivative is positive, the function is concave up (increasing). If it’s negative, the function is concave down (decreasing). It’s like having a superpower in math class.

Graphical Analysis

Don’t underestimate the power of visualizing the function. Graphing the function can give you a clear picture of where it’s increasing or decreasing. Plus, it’s a great way to double-check your work.

Tools and Resources to Help You

Let’s face it. Math can be tough sometimes. But luckily, there are tons of tools and resources out there to help you. Here are a few of our favorites:

Desmos: A free online graphing calculator that’s perfect for visualizing functions.
Khan Academy: A great resource for video tutorials and practice problems.
Symbolab: A powerful math solver that can walk you through step-by-step solutions.

These tools can save you tons of time and make learning a whole lot easier.

Real-Life Examples: Putting It All Together

Talking about math is one thing, but seeing it in action is another. Let’s look at a couple of real-life examples:

Example 1: Population Growth

Imagine you’re studying the population growth of a city over time. By analyzing the increasing and decreasing intervals of the population function, you can predict future trends and make informed decisions. Cool, right?

Example 2: Stock Market Analysis

In the stock market, understanding increasing and decreasing intervals can help investors make smarter decisions. By analyzing the behavior of stock prices, they can identify trends and capitalize on opportunities.

Tips for Mastering the Concept

Finally, here are a few tips to help you master how to find increasing decreasing intervals:

Practice, practice, practice. The more problems you solve, the better you’ll get.
Use visual aids like graphs and charts to help you understand the concepts.
Don’t be afraid to ask for help. Whether it’s from a teacher, tutor, or online resource, there’s no shame in seeking assistance.

Remember, mastering math takes time and effort. But with the right mindset and resources, you can do it.

Conclusion: Take Action and Keep Learning

And there you have it, folks. A comprehensive guide on how to find increasing decreasing intervals. From understanding the basics to mastering advanced techniques, we’ve covered it all. But the journey doesn’t stop here. Keep practicing, keep learning, and most importantly, keep asking questions.

Call to Action: Now it’s your turn. Share your thoughts in the comments below. Did you find this guide helpful? What challenges are you facing in your math journey? Let’s start a conversation and help each other grow.

And don’t forget to check out our other articles for more math tips and tricks. Happy learning, and see you in the next one!

What Are Increasing and Decreasing Intervals Anyway?
Why Should You Care About Increasing Decreasing Intervals?
Step-by-Step Guide: How to Find Increasing Decreasing Intervals
Common Mistakes to Avoid
Advanced Techniques: Beyond the Basics
Tools and Resources to Help You
Real-Life Examples: Putting It All Together
Tips for Mastering the Concept
Conclusion: Take Action and Keep Learning

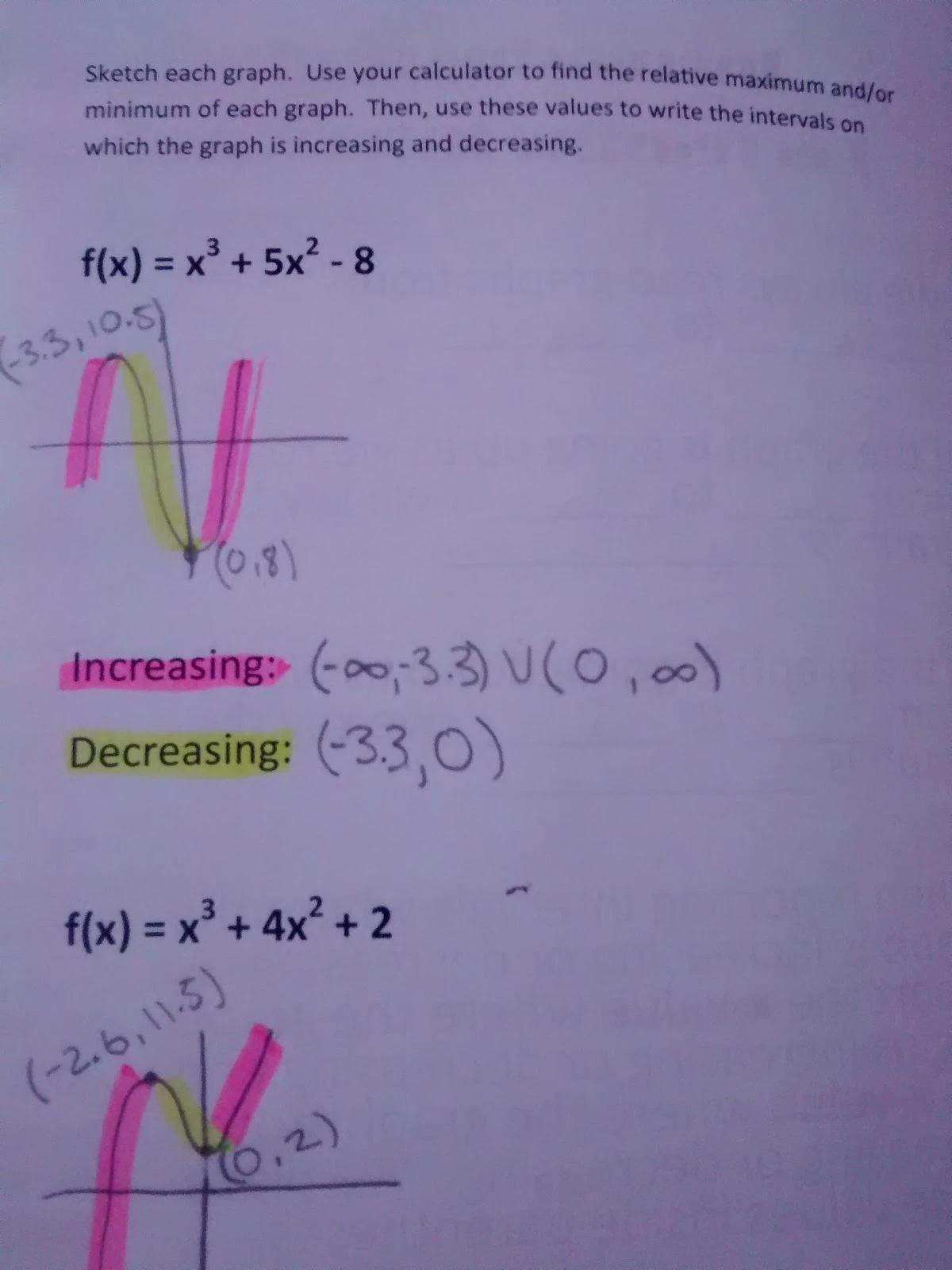
Increasing and Decreasing Intervals Foldable Math = Love

Increasing And Decreasing Intervals

Increasing Decreasing Intervals astonishingceiyrs

Celebrity Scandals