Mastering Decreasing Increasing Intervals: The Ultimate Guide
Alright, buckle up, folks! If you're diving headfirst into the world of mathematics or calculus, you've probably stumbled upon the term "decreasing increasing intervals." It sounds like a tongue-twister, but trust me, it's a concept that can unlock some serious math magic. Whether you're a student trying to ace your exams or a math enthusiast looking to sharpen your skills, understanding these intervals is crucial. So, let's break it down together, shall we?
Now, you might be thinking, "What's the big deal about intervals anyway?" Well, here's the scoop: Decreasing increasing intervals are like the secret sauce in calculus. They help us understand how functions behave—whether they're climbing up or diving down. And let's face it, in the real world, knowing how things change is pretty darn important, right?
So, without further ado, let's dive into this topic. By the end of this article, you'll not only know what decreasing increasing intervals are but also how to spot them, analyze them, and even apply them to real-life scenarios. Ready to level up your math game? Let's go!
- Brent Riveras Gf The Inside Scoop Yoursquove Been Waiting For
- Haircut For Square Face Your Ultimate Guide To Finding The Perfect Style
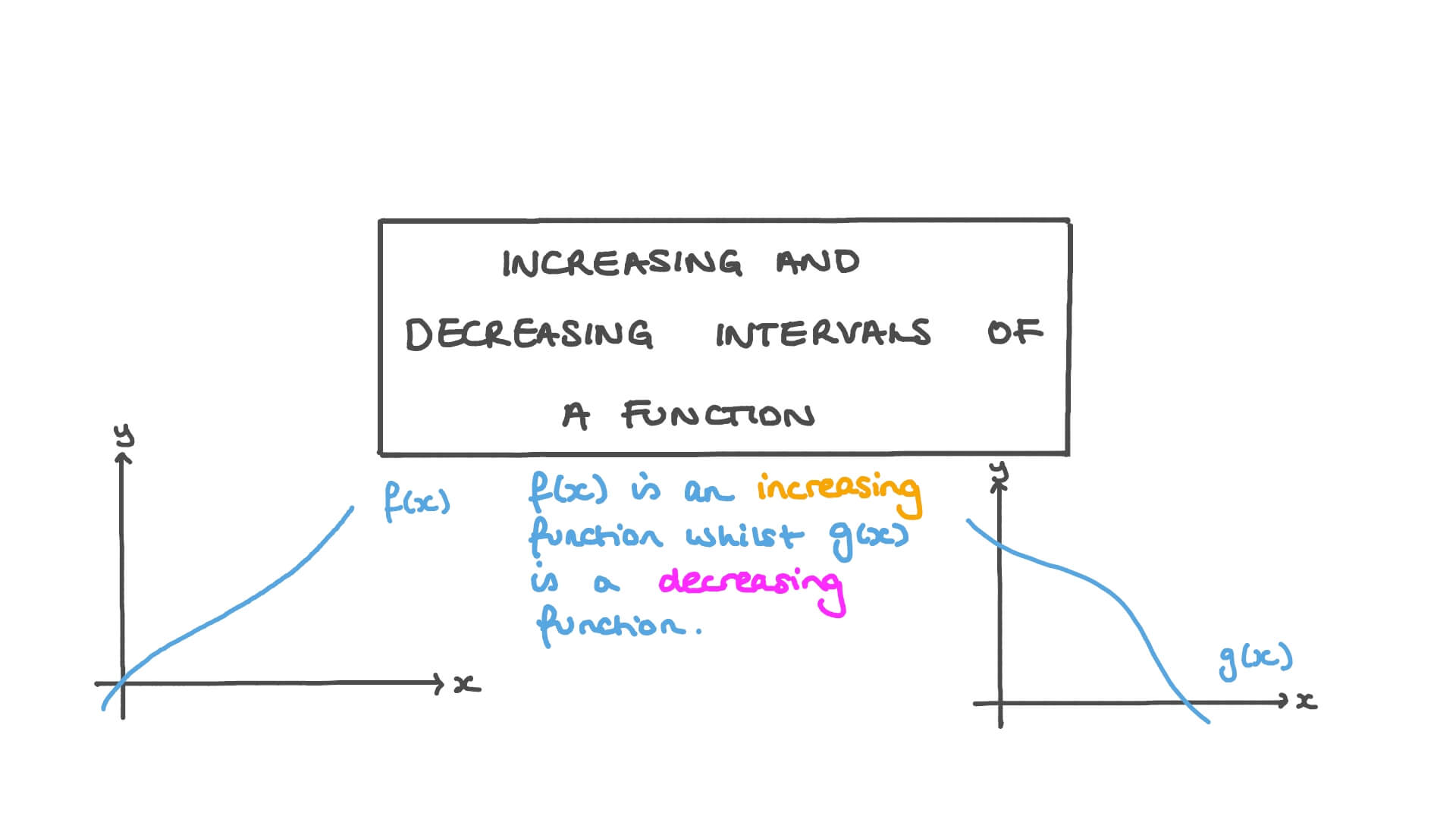
What Are Decreasing Increasing Intervals Anyway?
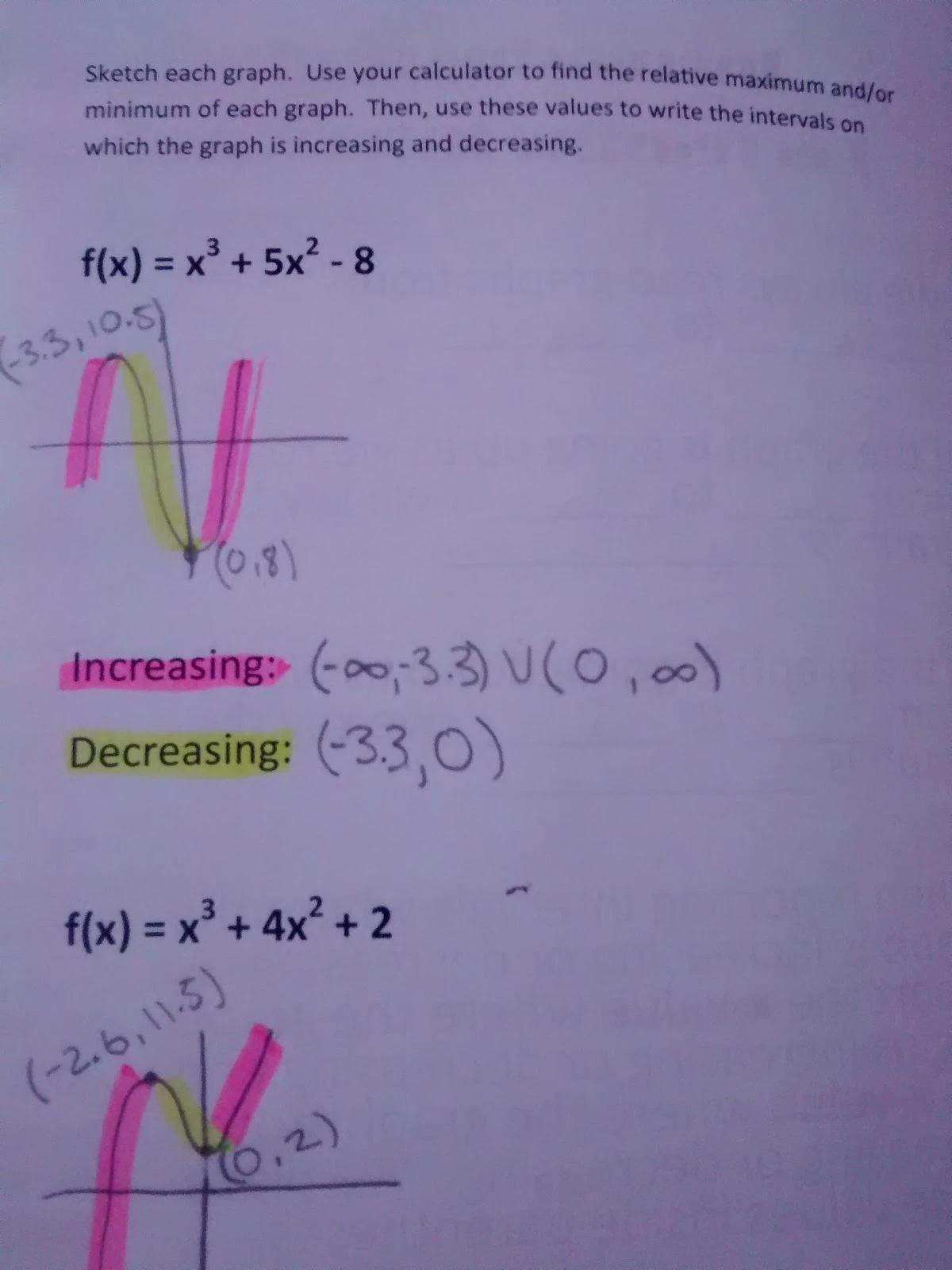
Alright, let's start with the basics. Decreasing increasing intervals refer to the sections of a function where the values either rise or fall. It's like watching a rollercoaster—sometimes it goes up, sometimes it goes down. But how do we figure out these intervals? That's where calculus comes in.
When we talk about increasing intervals, we're talking about the parts of the graph where the function is moving upward. On the flip side, decreasing intervals are where the function is heading south. Think of it as a mountain range: the peaks are the increasing parts, and the valleys are the decreasing parts.
Why Should You Care About These Intervals?
Here's the deal: understanding decreasing increasing intervals isn't just about acing a math test. It's about grasping how change works. Whether you're analyzing stock prices, predicting weather patterns, or even optimizing business strategies, knowing when something is increasing or decreasing can give you a serious edge.
- Aja Wilson Boyfriend The Untold Story Behind The Wnba Stars Love Life
- Wheres The Party At Discover The Location Of Cma Awards
For instance, imagine you're running a business and you want to know when your profits are peaking or dipping. By analyzing the intervals, you can make informed decisions about when to expand or cut costs. Cool, right?
How to Identify Decreasing Increasing Intervals
Alright, let's get practical. Identifying these intervals isn't rocket science, but it does require a bit of know-how. First things first, you'll need to find the derivative of the function. The derivative tells us the rate of change at any given point. If the derivative is positive, the function is increasing. If it's negative, the function is decreasing. Simple, right?
Here's a quick breakdown:
- Positive derivative = Increasing interval
- Negative derivative = Decreasing interval
Step-by-Step Guide to Spotting Intervals
Let me walk you through the process. Say you have a function like f(x) = x^2. To find the intervals, follow these steps:
- Find the derivative: f'(x) = 2x
- Set the derivative equal to zero to find critical points: 2x = 0 → x = 0
- Test intervals around the critical points to determine if the derivative is positive or negative
Once you've done that, you'll have a clear picture of where the function is increasing or decreasing. It's like putting together a puzzle, piece by piece.
Practical Applications of Decreasing Increasing Intervals
Now that you know how to identify these intervals, let's talk about how they apply to the real world. From economics to physics, decreasing increasing intervals are everywhere. Here are a few examples:
In economics, businesses use these intervals to analyze supply and demand. By understanding when prices are rising or falling, companies can adjust their strategies accordingly. In physics, scientists use intervals to study motion and acceleration. Even in biology, researchers use these concepts to model population growth and decline.
Real-Life Example: Stock Market Analysis
Let's zoom in on the stock market. Traders use decreasing increasing intervals to predict trends. By analyzing the rate of change in stock prices, they can make informed decisions about when to buy or sell. It's like having a crystal ball that tells you when the market is about to take off or crash.
Common Mistakes to Avoid
Alright, let's talk about the pitfalls. One of the most common mistakes people make is not testing the intervals correctly. Just because the derivative is zero at a certain point doesn't mean the function is automatically increasing or decreasing. You have to test the intervals around that point to be sure.
Another mistake is overcomplicating things. Sometimes, the simplest approach is the best. Don't get bogged down in unnecessary calculations. Stick to the basics and you'll be golden.
Pro Tip: Keep It Simple
Here's a little secret: the best mathematicians are the ones who can break complex problems into simple steps. Don't try to reinvent the wheel. Use the tools you have and practice, practice, practice. The more you work with these intervals, the more intuitive they'll become.
Advanced Techniques for Analyzing Intervals
For those of you who want to take things to the next level, there are some advanced techniques you can use. One of them is the second derivative test. This test helps you determine whether a critical point is a maximum, minimum, or neither. It's like having a superpower for analyzing functions.
Here's how it works: if the second derivative is positive at a critical point, the function has a local minimum. If it's negative, the function has a local maximum. If it's zero, well, you're back to square one.
Why the Second Derivative Test Matters
The second derivative test is more than just a fancy tool. It gives you a deeper understanding of how functions behave. By knowing whether a point is a maximum or minimum, you can make more accurate predictions about the function's behavior. And in the world of math, accuracy is key.
Tools and Resources for Learning
Alright, let's talk tools. Whether you're a visual learner or someone who prefers hands-on practice, there are plenty of resources out there to help you master decreasing increasing intervals. From online calculators to interactive graphs, the options are endless.
Some of my personal favorites include Desmos for graphing functions and Khan Academy for step-by-step tutorials. These tools not only make learning fun but also help reinforce the concepts in a practical way.
Top Resources to Check Out
- Desmos: Interactive graphing calculator
- Khan Academy: Free video tutorials
- Wolfram Alpha: Advanced math solver
Conclusion: Leveling Up Your Math Game
And there you have it, folks! Decreasing increasing intervals might seem intimidating at first, but with the right approach, they're totally doable. By understanding how functions behave, you can unlock a whole new world of possibilities. Whether you're a student, a professional, or just a curious learner, these concepts have something to offer everyone.
So, what's next? I challenge you to take what you've learned and apply it to a real-world problem. Maybe analyze the stock market, or study a physics problem. The more you practice, the better you'll get. And remember, math isn't just about numbers—it's about understanding the world around us.
Before you go, drop a comment below and let me know what you think. Did this article help you? What other math topics would you like to explore? And don't forget to share this with your friends—knowledge is power, after all!
Table of Contents
- What Are Decreasing Increasing Intervals Anyway?
- Why Should You Care About These Intervals?
- How to Identify Decreasing Increasing Intervals
- Step-by-Step Guide to Spotting Intervals
- Practical Applications of Decreasing Increasing Intervals
- Real-Life Example: Stock Market Analysis
- Common Mistakes to Avoid
- Pro Tip: Keep It Simple
- Advanced Techniques for Analyzing Intervals
- Why the Second Derivative Test Matters
- Tools and Resources for Learning
- Top Resources to Check Out
- Conclusion: Leveling Up Your Math Game
- What Is Alanon Meaning Unlock The Secrets To Support And Recovery
- Unlocking The World Of Vanilla Gift Card Numbers What You Need To Know
Increasing and Decreasing Intervals Foldable Math = Love

Increasing And Decreasing Intervals
Increasing Decreasing Intervals astonishingceiyrs